Advection solvers¶
The linear advection equation:
provides a good basis for understanding the methods used for compressible hydrodynamics. Chapter 4 of the notes summarizes the numerical methods for advection that we implement in pyro.
pyro has several solvers for linear advection, which solve the equation with different spatial and temporal intergration schemes.
advection solver¶
advection implements the directionally unsplit corner
transport upwind algorithm [Colella90] with piecewise linear reconstruction.
This is an overall second-order accurate method, with timesteps restricted
by
The parameters for this solver are:
section: [advection]
option
value
description
u
1.0advective velocity in x-direction
v
1.0advective velocity in y-direction
limiter
2limiter (0 = none, 1 = 2nd order, 2 = 4th order)
section: [driver]
option
value
description
cfl
0.8advective CFL number
section: [particles]
option
value
description
do_particles
0particle_generator
grid
advection_fv4 solver¶
advection_fv4 uses a fourth-order accurate finite-volume
method with RK4 time integration, following the ideas in
[McCorquodaleColella11]. It can be thought of as a
method-of-lines integration, and as such has a slightly more restrictive
timestep:
The main complexity comes from needing to average the flux over the faces of the zones to achieve 4th order accuracy spatially.
The parameters for this solver are:
section: [advection]
option
value
description
u
1.0advective velocity in x-direction
v
1.0advective velocity in y-direction
limiter
1limiter (0 = none, 1 = ppm)
temporal_method
RK4integration method (see mesh/integrators.py)
section: [driver]
option
value
description
cfl
0.8advective CFL number
advection_nonuniform solver¶
advection_nonuniform models advection with a non-uniform
velocity field. This is used to implement the slotted disk problem
from [Zal79]. The basic method is similar to the
algorithm used by the main advection solver.
The paramters for this solver are:
section: [advection]
option
value
description
u
1.0advective velocity in x-direction
v
1.0advective velocity in y-direction
limiter
2limiter (0 = none, 1 = 2nd order, 2 = 4th order)
section: [driver]
option
value
description
cfl
0.8advective CFL number
section: [particles]
option
value
description
do_particles
0particle_generator
grid
advection_rk solver¶
advection_rk uses a method of lines time-integration
approach with piecewise linear spatial reconstruction for linear
advection. This is overall second-order accurate, so it represents a
simpler algorithm than the advection_fv4 method (in particular, we
can treat cell-centers and cell-averages as the same, to second
order).
The parameter for this solver are:
section: [advection]
option
value
description
u
1.0advective velocity in x-direction
v
1.0advective velocity in y-direction
limiter
2limiter (0 = none, 1 = 2nd order, 2 = 4th order)
temporal_method
RK4integration method (see mesh/integrators/.py)
section: [driver]
option
value
description
cfl
0.8advective CFL number
advection_weno solver¶
advection_weno uses a WENO reconstruction and method of
lines time-integration
The main parameters that affect this solver are:
section: [advection]
option
value
description
u
1.0advective velocity in x-direction
v
1.0advective velocity in y-direction
limiter
0Unused here, but needed to inherit from advection base class
weno_order
3k in WENO scheme
temporal_method
RK4integration method (see mesh/integrators/.py)
section: [driver]
option
value
description
cfl
0.5advective CFL number
General ideas¶
The main use for the advection solver is to understand how Godunov techniques work for hyperbolic problems. These same ideas will be used in the compressible and incompressible solvers. This video shows graphically how the basic advection algorithm works, consisting of reconstruction, evolution, and averaging steps:
Examples¶
smooth¶
The smooth problem initializes a Gaussian profile and advects it with \(u = v = 1\) through periodic boundaries for a period. The result is that the final state should be identical to the initial state—any disagreement is our numerical error. This is run as:
./pyro.py advection smooth inputs.smooth
By varying the resolution and comparing to the analytic solution, we
can measure the convergence rate of the method. The smooth_error.py
script in analysis/ will compare an output file to the analytic
solution for this problem.
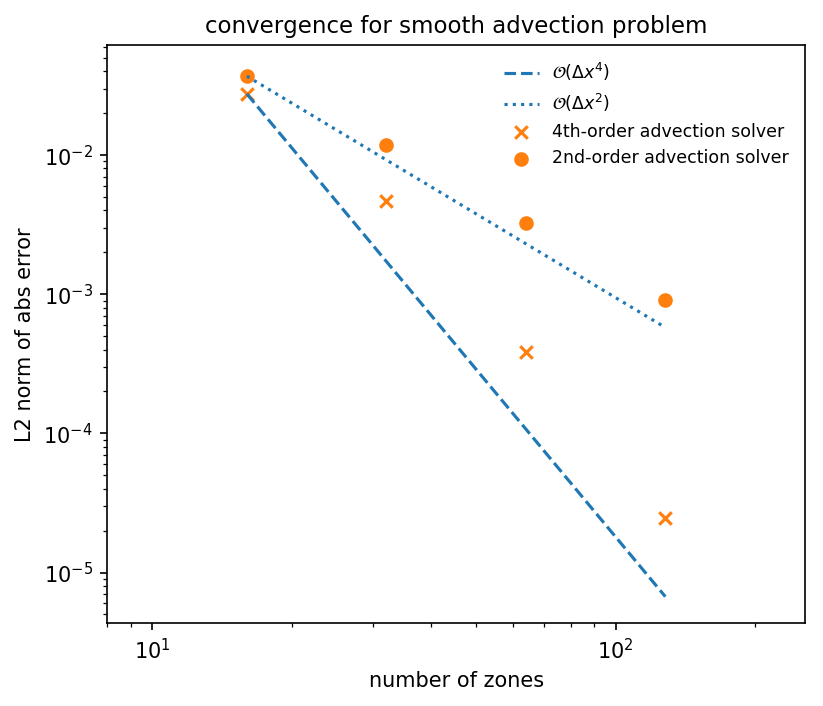
The points above are the L2-norm of the absolute error for the smooth
advection problem after 1 period with CFL=0.8, for both the
advection and advection_fv4 solvers. The dashed and dotted
lines show ideal scaling. We see that we achieve nearly 2nd order
convergence for the advection solver and 4th order convergence
with the advection_fv4 solver. Departures from perfect scaling
are likely due to the use of limiters.
tophat¶
The tophat problem initializes a circle in the center of the domain with value 1, and 0 outside. This has very steep jumps, and the limiters will kick in strongly here.
Exercises¶
The best way to learn these methods is to play with them yourself. The exercises below are suggestions for explorations and features to add to the advection solver.
Explorations¶
Test the convergence of the solver for a variety of initial conditions (tophat hat will differ from the smooth case because of limiting). Test with limiting on and off, and also test with the slopes set to 0 (this will reduce it down to a piecewise constant reconstruction method).
Run without any limiting and look for oscillations and under and overshoots (does the advected quantity go negative in the tophat problem?)
Extensions¶
Implement a dimensionally split version of the advection algorithm. How does the solution compare between the unsplit and split versions? Look at the amount of overshoot and undershoot, for example.
Research the inviscid Burger’s equation—this looks like the advection equation, but now the quantity being advected is the velocity itself, so this is a non-linear equation. It is very straightforward to modify this solver to solve Burger’s equation (the main things that need to change are the Riemann solver and the fluxes, and the computation of the timestep).
The neat thing about Burger’s equation is that it admits shocks and rarefactions, so some very interesting flow problems can be setup.